Buenos días, hoy vamos a seguir realizando ejercicios de estadística y reforzar las medidas de centralización: media, moda y mediana.
Problema 1
Las notas del examen de matemáticas de 15 alumnos son las siguientes: 5, 3, 9, 7, 3, 6, 7, 5, 8, 7, 5, 4, 7, 6 y 8.
Calcular la media, moda y mediana de las notas.
Solución
Para calcular la media, sumamos las notas y dividimos entre 15:
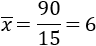Ordenamos los datos de menor a mayor:
Como hay 15 datos (número impar), la mediana es el dato de la posición . La mediana es 6.
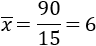
3, 3, 4, 5, 5, 5, 6, 6, 7, 7, 7, 7, 8, 8, 9
La moda es 7 (es la nota que más se repite).Como hay 15 datos (número impar), la mediana es el dato de la posición . La mediana es 6.
Problema 2
La siguiente tabla proporciona el número de gatos y de perros que tienen en casa un grupo de 10 amigos:
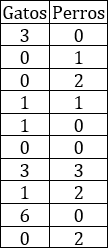
- Calcular la media, moda y mediana del número gatos.
- Lo mismo con el número de perros.
- Si sumamos el número de gatos y de perros, tenemos el número de mascotas de cada amigo. Calcular la media, moda y mediana de este dato.
Nota: Fijaros que son dos conjuntos de datos, gatos y perros. No confundirlo con las tablas en las que aparecen los datos y las frecuencias.
Solución
a. La media del número de gatos es 1.5, la moda es 0 y la mediana es 1.
b. La media del número de perros es 1.1, la moda es 0 y la mediana es 1.
c. Tenemos que sumar los datos de la tabla por filas, obteniendo los datos 3, 1, 2, 2, 1, 0, 6, 3, 6, 2. La media es 2.6, la moda es 2 y la mediana es 2.
b. La media del número de perros es 1.1, la moda es 0 y la mediana es 1.
c. Tenemos que sumar los datos de la tabla por filas, obteniendo los datos 3, 1, 2, 2, 1, 0, 6, 3, 6, 2. La media es 2.6, la moda es 2 y la mediana es 2.
Problema 3
El profesor de gimnasia anotó el número de goles que marcaron sus 50 alumnos:
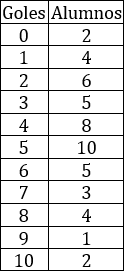
- Representar la gráfica número de alumnos en función del número de goles que marcaron.
- Calcular la media, moda y mediana del número de goles.
- ¿Cuántos alumnos marcaron un número de goles menor que la mediana? ¿Y mayor?
Solución
a. Gráfica
En el eje horizontal escribimos el número de goles y en el eje vertical, el de alumnos:
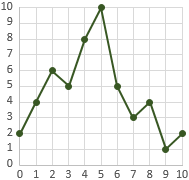b. Media
Como tenemos que sumar los datos y algunos de ellos se repiten, podemos multiplicar goles por alumnos y sumar los resultados. Después, dividimos entre el total de alumnos, que es 50:
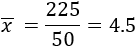Moda
El número de goles que más se repite es 5 (10 de los 50 alumnos marcaron 5 goles). Por tanto, la moda es 5.
Mediana
Como hay 50 alumnos (número par), la mediana es la media de los dos datos centrales (los que ocupan las posiciones 25 y 26). Estas posiciones corresponden a 4 y 5 goles. Por tanto, la mediana es 4.5.
c. 25 alumnos marcaron un número de goles menor que la mediana y los otros 25 marcaron un número superior.
En el eje horizontal escribimos el número de goles y en el eje vertical, el de alumnos:
Como tenemos que sumar los datos y algunos de ellos se repiten, podemos multiplicar goles por alumnos y sumar los resultados. Después, dividimos entre el total de alumnos, que es 50:
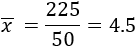
El número de goles que más se repite es 5 (10 de los 50 alumnos marcaron 5 goles). Por tanto, la moda es 5.
Mediana
Como hay 50 alumnos (número par), la mediana es la media de los dos datos centrales (los que ocupan las posiciones 25 y 26). Estas posiciones corresponden a 4 y 5 goles. Por tanto, la mediana es 4.5.
c. 25 alumnos marcaron un número de goles menor que la mediana y los otros 25 marcaron un número superior.
No hay comentarios:
Publicar un comentario