Buenos días chic@s, vamos a empezar con un ejercicio:
Un ciclista sale de excursión a un lugar que dista 20 km de su casa. A los 15 minutos de la salida, cuando se encuentran a 6 km, hace una parada de 10 minutos. Reanuda la marcha y llega a su destino una hora después de haber salido de casa.
Representa la gráfica tiempo–distancia a su casa, suponiendo que la velocidad es constante en cada tramo.
Sol:
Ahora vamos a avanzar un poco más y ver las funciones desde un punto de vista más analítico.
En multitud de ocasiones las funciones vienen expresadas mediante fórmulas. Llamaremos expresión analítica de una función a la fórmula que relaciona la variable dependiente con la variable independiente, es decir, una expresión que me permite hallar la imagen de cada valor de la variable independiente x sin más que sustituir la x por su valor.
Por ejemplo:
a) f(x)=2x-1, la función viene expresada por la expresión analítica 2x-1
¿Cual sería la imagen de x=1?
Pues la obtendría sustituyendo x por 1, es decir, f(1)=2·1-1=1
¿Y la imagen del 3?
f(3)=2·3-1=5
b)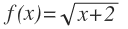
¿Cuál sería la imagen de x=7?
b)
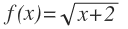
¿Cuál sería la imagen de x=7?
Pues tenemos que cambiar la x por 7 y obtenemos f(7)=3
Os podéis imaginar que existen infinidad de funciones, tanto como fórmulas nos podamos imaginar.
Os dejo este link para que podáis poner las fórmulas que queráis y ver como son sus gráficas (elevar al cuadrado se hace con el símbolo ^), si vais cambiando la ecuación os irá cambiando la gráfica:
http://fooplot.com/?lang=es#W3sidHlwZSI6MCwiZXEiOiIyeCsxIiwiY29sb3IiOiIjMDAwMDAwIn0seyJ0eXBlIjoxMDAwfV0
FUNCIÓN LINEAL
Dentro de todas esas funciones nos vamos a centrar primero en la función lineal:
Una función lineal es una función polinómica de primer grado. Es decir, tiene la siguiente forma
siendo m≠0.
- m es la pendiente de la función (Si es positiva será una recta creciente y si es negativa será decreciente) En el caso de que m sea 0 la recta será una recta paralela al eje x pasando por el punto (0,n).
- n es la ordenada (en el origen) de la función, es decir el punto de corte con el eje y
La gráfica de una función lineal es siempre una recta. Para dibujarla haremos una tabla de valores.
Veamos el siguiente vídeo:
Ejemplo: Representar f(x)=2x-1
Lo primero es hacer una tabla de valores:
Si x=1 su imagen es 1
Si x=2 su imagen es 3
Si x= -1 su imagen es -3
Poniendo los puntos en unos ejes y uniéndolos nos queda:
La pendiente de la recta es m = 2 que es positiva por tanto es una recta creciente y la ordenada es n = -1 lo que significa que corta al eje "y" en el punto -1.
Podéis preguntaros como hago para elegir las x, pues la representación no depende de las coordenadas de x que elijáis, cada uno puede elegir las que quiera, normalmente se suelen coger números positivos, negativos y cero.
Podéis preguntaros como hago para elegir las x, pues la representación no depende de las coordenadas de x que elijáis, cada uno puede elegir las que quiera, normalmente se suelen coger números positivos, negativos y cero.
Ejercicios:
1Representar gráficamente 

2. Representar gráficamente 

SOLUCIONES:
1 Representar gráficamente 

Le damos valores a la función





Obtenemos la siguiente tabla de valores
| X | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Y |  |  |  |  |  |

El punto (0, 3) es la ordenada en el origen. La pendiente es m=2 y por lo tanto ya podéis comprobar que se cumple la teoría, la recta es creciente.
2. Representar gráficamente 

Le damos valores a la función x=0 y x=4 y hallamos las imágenes


 |  |
|---|---|
 |  |
 |  |
Los representamos y unimos los puntos:

El punto  es la ordenada en el origen. Fijaros que es una recta decreciente ya que la pendiente es m=-3/4 que es negativa.
es la ordenada en el origen. Fijaros que es una recta decreciente ya que la pendiente es m=-3/4 que es negativa.
 es la ordenada en el origen. Fijaros que es una recta decreciente ya que la pendiente es m=-3/4 que es negativa.
es la ordenada en el origen. Fijaros que es una recta decreciente ya que la pendiente es m=-3/4 que es negativa.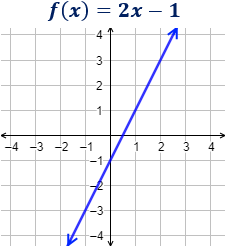
No hay comentarios:
Publicar un comentario